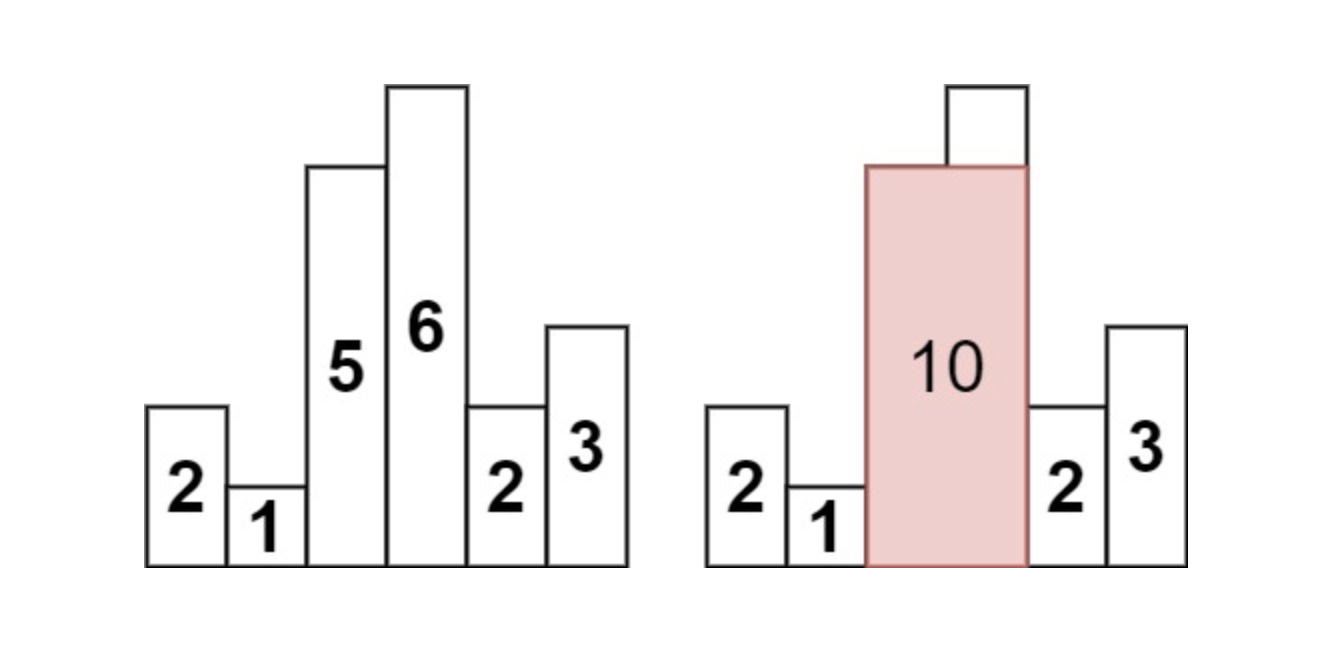
히스토그램에서 가장 큰 직사각형
General / Algorithms

히스토그램에서 가장 큰 직사각형

히스토그램에서 가장 큰 직사각형(Largest Rectangle in Histogram)이라는 문제를 푸는 다양한 방법에 대해 알아보자.

이 문제는 임의의 높이를 가진 $N$개의 막대가 주어질 때, 막대 안에 포함되는 직사각형 중 가장 넓이가 큰 직사각형의 넓이를 구하는 유명한 문제인데, 푸는 방법이 다양하다는 점에서 재미있다.

유명한 문제이기 때문에 다양한 온라인 저지 사이트에서 이 문제가 올라와 있는 것을 볼 수 있다. 문제마다 입력으로 주어지는 값들의 조건은 조금씩 다르기도 하다.

여기서는 LeetCode 84. Largest Rectangle in Histogram 를 기준으로 설명하겠다.

본 글에서는 이 문제를 해결하는 5가지 풀이에 대해 알아볼 것이다.

풀이

브루트포스

시간복잡도 : $O(N^3)$

우선 알고리즘의 효율성에 대해 생각하지 말고 가장 무식한 방법을 떠올려보자. 만들 수 있는 모든 직사각형을 만들어 직사각형의 넓이를 구하면 답을 계산할 수 있을 것이다. 모든 직사각형은 자신의 가장 왼쪽에 위치한 막대와 가장 오른쪽에 위치한 막대가 있을 것이다. 그 직사각형의 높이는 위치상 직사각형에 포함되는 막대들의 높이 중 가장 낮은 막대의 높이가 될 것이다. 그렇기 때문에 모든 막대 쌍 l, r 에 대해 l 부터 r 까지의 막대 중 가장 높이가 낮은 막대의 높이를 계산한 뒤 직사각형의 넓이를 계산해 답을 갱신하면 문제를 해결할 수 있다.

모든 막대 쌍을 순회하는 데 $O(N^2)$ 의 시간이 소요되고, 각 막대 쌍에 대해 최대 높이를 구하는데 $O(N)$ 의 시간이 소요되므로, 총 $O(N^3)$ 의 시간이 소요된다.

class Solution {
    const int MAX_H = 10000;
public:
    int largestRectangleArea(vector<int>& heights) {
        int N = heights.size();
        int ans = 0;
        for(int i = 0; i < N; i++) {
            for(int j = i; j < N; j++) {
                int minH = MAX_H + 1;
                for(int k = i; k <= j; k++) {
                    minH = min(minH, heights[k]);
                }
                ans = max(ans, (j - i + 1) * minH);
            }
        }
        return ans;
    }
};

최적화된 브루트포스

시간복잡도 : $O(N^2)$

앞서 설명한 알고리즘을 다시 한 번 보자. 첫번째 반복문에서 왼쪽 막대를 정하고, 두번째 반복문에서 오른쪽 막대를 정하게 된다. 그런데 직사각형의 높이를 찾기위한 세번째 반복문을 잘 보면, 오른쪽 막대를 오른쪽으로 한 칸씩 이동할 때마다 매번 맨 왼쪽 막대부터 처음부터 확인하는 것을 알 수 있다. 굳이 이미 봤던 막대를 다시 볼 필요가 없기 때문에 두번째와 세번째 반복문을 하나의 반복문으로 합칠 수가 있다. 그리하여 시간복잡도는 $O(N^2)$ 이 된다.

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int N = heights.size();
        int ans = -1;

        for(int i = 0; i < N; i++) {
            int minH = heights[i];
            for(int j = i; j < N; j++) {
                minH = min(minH, heights[j]);
                ans = max(ans, (j - i + 1) * minH);
            }
        }
        return ans;
    }
};

세그먼트 트리

시간복잡도 : $O(NlogH)$

이번에는 문제를 다르게 한 번 정의해 보자. 앞에서는 양쪽 막대의 가능한 쌍을 모두 확인했기 때문에 그것만으로도 $O(N^2)$ 의 시간복잡도가 소요되었다.

하지만 잘 생각해보면 히스토그램 안에 있는 직사각형들은 높이를 가지고, 직사각형 안에는 항상 직사각형과 같은 높이를 가지는 막대가 있을 것이다.

그렇기 때문에 이번에는 높이가 되는 막대를 정하고 그 높이를 가지는 직사각형 중 가장 큰 직사각형을 찾아보자. 즉, 정해진 높이를 가질 수 있는 가장 왼쪽 막대와 가장 오른쪽 막대를 찾아보자.

문제를 단순화하기 위해 왼쪽과 오른쪽 중에 일단 왼쪽부터 보자.

즉, 각 막대에 대해 해당 막대의 높이로 직사각형을 만들 수 있는 가장 왼쪽 막대의 인덱스를 찾아보자.

살짝 다르게 말해서, (1) 나보다 왼쪽에 있는 막대 중, (2) 나보다 낮은 막대 중에 (3) 가장 오른쪽에 있는 막대를 찾아보자. 그럼 그 막대의 오른쪽 막대가 현재 보는 기둥의 높이로 만들 수 있는 직사각형의 가장 왼쪽 막대가 된다.

그럼 maxIdx 라는 배열을 만들어 maxIdx[i] 를 i의 높이를 가지는 막대들의 index 중 최대값이라고 정의해보자.

막대는 왼쪽부터 오른쪽으로 봐 나갈 것이고, 막대를 볼 때마다 해당 막대의 높이 정보로 maxIdx 를 업데이트한다고 하면, 결국 1번 조건은 자동으로 만족되고, 2번과 3번 조건은 RMQ(Range Maximum Query) 를 통해 로그 시간으로 계산할 수 있다. 쿼리를 수행하는 범위(range)는 [0, 직사각형 높이 - 1] 이 된다. 여기서 주의해야할 점은, 문제에서 주어지는 막대의 최대 높이가 너무 커서 세그먼트 트리를 구축할 수 없는 경우다. 하지만, 막대의 개수는 충분히 작을 것이기 때문에(대부분의 경우는 $10^5$ 이하) 좌표 압축을 수행하면 된다. 여기서는 막대의 최대 높이가 $10^4$ 라고 가정하겠다. 아무튼 이렇게 하여 막대의 최대 높이가 $H$ 일 때, $O(NlogH)$ 의 시간복잡도로 각 막대를 높이로 삼는 직사각형의 왼쪽 끝 막대를 찾을 수 있었다.

이번엔 오른쪽 끝 막대를 찾아볼 텐데, 사실 잘 생각해보면 막대의 순서를 뒤집어서 같은 일을 하면 된다.

여기서 오른쪽 끝 막대의 경우 계산하고 난 뒤에 배열과 인덱스들을 다시 뒤집어 주는 것을 잊으면 안된다.

결론적으로, 세그먼트 트리를 구축하는데 $O(H)$ 의 시간이 걸리고 각 높이 별 왼쪽 끝 막대와 오른쪽 끝 막대의 인덱스를 찾는데 각각 $O(NlogH)$ 의 시간 복잡도가 걸려서, 전체 시간 복잡도는 $O(H + NlogH)$ 다. 물론, 여기서 $H$ 가 커진다면 $O(NlogN)$ 으로 좌표압축을 해야하지만, 지금은 $H < N$ 이기 때문에, 무시해도 될 것이다. 즉, 최종 시간복잡도는 $O(NlogH)$.

class Solution {
    int MAX_H = 10000;
    int maxRange = 1;
    vector<int> tree;
    vector<int> lBorders;
    vector<int> rBorders;
public:
    Solution() {
        while(maxRange < MAX_H) maxRange *= 2;
        tree = vector<int>(maxRange * 2, -1);
    }
    void update(int pos, int val) {
        pos += maxRange;
        tree[pos] = max(tree[pos], val);
        for(; pos > 1; pos /= 2) {
            tree[pos / 2] = max(tree[pos], tree[pos ^ 1]);
        }
    }
    int query(int l, int r) {
        l += maxRange, r += maxRange;
        int ret = -1;
        for(; l <= r; l /= 2, r /= 2) {
            if(l & 1) ret = max(ret, tree[l++]);
            if(~r & 1) ret = max(ret, tree[r--]);
        }
        return ret;
    }
    void solve(vector<int>& heights, vector<int>& borders) {
        for(int i = 0; i < heights.size(); i++) {
            borders[i] = query(0, heights[i] - 1);
            update(heights[i], i);
        }
    }
    int largestRectangleArea(vector<int>& heights) {
        int N = heights.size();
        lBorders = vector<int>(N, 0);
        rBorders = vector<int>(N, 0);
        int ans = -1;

        solve(heights, lBorders);

        vector<int> reversed = heights;
        reverse(begin(reversed), end(reversed));
        tree = vector<int>(2 * maxRange, -1);

        solve(reversed, rBorders);
        reverse(begin(rBorders), end(rBorders));
        for(int i = 0; i < N; i++) rBorders[i] = N - rBorders[i] - 1;

        for(int i = 0; i < N; i++) {
            ans = max(ans, (rBorders[i] - lBorders[i] - 1) * heights[i]);
        }
        return ans;
    }
};

분할정복 + 그리디

시간복잡도 : $O(NlogN)$

재귀적으로 문제를 해결해보자. 일단 $N$ 개의 막대로 이루어진 임의의 히스토그램이 주어졌을 때 막대들을 절반으로 나누어보자. 히스토그램 내 직사각형은 3가지 경우 중 하나일 것이다. (1) 왼쪽 절반에 있거나, (2) 오른쪽 절반에 있거나, (3) 사이에 걸쳐있거나. 그럼 (1)번과 (2)번의 경우는 결국 일부 막대에 대해 완전히 동일한 문제를 푸는 것이 되기 때문에 재귀 호출로 간단히 해결할 수 있다. 그럼 (3)번의 경우만 계산해주면 문제를 해결할 수 있다. 풀이2 에서 썼던 무식한 방법으로도 계산할 수 있지만, 이러면 애초에 풀이2 로 푸는것보다도 비효율적이다. 여기서는 잘 생각해보면 다음과같이 그리디하게 $O(N)$ 으로 계산할 수가 있다.

왼쪽 끝 막대와 오른쪽 끝 막대를 2개의 포인터로 가리키게 해보자. 이 두 포인터를 가장 가운데 있는 두 막대를 가리키도록 초기화 하고 둘을 바깥쪽으로 하나씩 이동시키면서 답을 계산할 것이다. 매 단계마다 두 포인터 중에서 다음 막대의 높이가 더 높은 포인터를 이동시킨다. 그리고 새로 가리킨 막대의 높이로 직사각형의 높이를 갱신한다. 이렇게 했을 때 답을 구할 수 있다는 것을 증명해보자.

위의 알고리즘의 경우 매 반복마다 두 포인터 중 하나를 한 칸 이동시키기 때문에 직사각형의 너비는 항상 1만큼 증가한다. 중요한 것은 높이의 변화인데, 다음 4가지 상황으로 나눌 수 있다.

  • (1) 만약 왼쪽 포인터와 오른쪽 포인터 모두에 대해 다음 막대가 현재 직사각형의 높이보다 높거나 같은 높이인 경우

어느 포인터를 이동시키든 직사각형의 높이는 그대로 유지되기 때문에 어느쪽을 이동시키든 상관없다.

  • (2) 왼쪽 포인터와 오른쪽 포인터 모두, 다음 막대가 현재 직사각형의 높이보다 낮은 경우

이 경우에는 높이가 최소한으로 줄어들 수 있는 선택을 해야한다. 직사각형의 높이는 직사각형을 이루는 모든 막대들의 높이 중 최소값이므로 이 경우 직사각형의 높이는 새로 가리키게 되는 막대의 높이로 변한다. 그렇기 때문에 다음 막대의 높이가 더 큰 포인터를 이동시킨다.

  • (3) 한쪽은 직사각형의 높이보다 높거나 같고, 한쪽은 낮은 경우

높거나 같은 쪽으로 움직여야 직사각형의 높이가 줄어들지 않고 그대로 유지되므로 높이가 높은 쪽 포인터를 움직인다.

위의 방법은 직사각형의 높이가 가능한한 천천히 감소하도록 너비를 1씩 증가시켰기 때문에, 가능한 모든 너비에서 가장 높은 높이로 답을 계산하게 된다.

다르게 생각해보면, 직사각형의 높이는 절대 커지지 않는다. 만약 변한다면 작아지기만 한다. 그렇기 때문에 위의 알고리즘은 높이가 유지되는 선에서 최대한 양쪽 포인터를 바깥쪽으로 늘리게 되고, 작아져야만 하는 경우에는 최소한으로만 감소시키기 때문에 결국엔 모든 막대들을 높이로 내림차순 정렬한 배열에서, 초기 높이에서부터 하나씩 작아지는 방향으로 직사각형의 높이를 변화시키게 된다.

이 때 재귀함수 호출의 깊이는 최대 $logN$ 번이고, 각 함수에서는 전체 막대기를 한 번씩 보게 된다. 그렇기 때문에 각 재귀 단계마다 전체 막대를 한 번씩 확인하는 셈이며, 그래서 전체 시간 복잡도는 $O(NlogN)$ 이다.

class Solution {
    const int MAX_H = 10000;
    vector<int> heights;

    int solve(int left, int right) {
        if(left == right) return heights[left];
        int mid = left + (right - left) / 2;
        int ans = max(solve(left, mid), solve(mid + 1, right));

        int lpos = mid, rpos = mid + 1;
        int minH = MAX_H + 1;
        while(left <= lpos && rpos <= right) {
            minH = min({minH, heights[lpos], heights[rpos]});
            ans = max(ans, (rpos - lpos + 1) * minH);
            if(left == lpos) ++rpos;
            else if(right == rpos) --lpos;
            else if(heights[lpos - 1] <= heights[rpos + 1]) ++rpos;
            else --lpos;
        }
        return ans;
    }
public:
    int largestRectangleArea(vector<int>& heights) {
        this->heights = heights;
        return solve(0, heights.size() - 1);
    }
};

스택

시간복잡도 : $O(N)$

이번에도 마찬가지로 각 막대의 높이를 기둥으로 하는 직사각형의 가장 왼쪽 막대와 가장 오른쪽 막대를 찾아볼 것이다. 여기서는 스택을 사용하여 왼쪽 막대부터 보면서 하나씩 스택에 넣어줄 건데, 이 막대를 높이로하는 직사각형의 넓이의 계산은 나중으로 미루게 된다. 언제 계산하냐면, 이 막대보다 작은 높이의 막대를 발견하는 즉시 계산해준다. 왜냐하면 발견한 막대가 바로 앞서 스택에 넣었던 막대보다 오른쪽에 있으면서 높이가 작은 가장 왼쪽 막대이기 때문이다. 직사각형 넓이의 계산과 동시에 해당 막대는 스택에서 빼준다. 해당 막대를 높이로 하는 직사각형을 이미 계산했기 때문이다. 이런 방식으로 스택을 관리해주면 자연스레 스택에 있는 막대들은 높이가 오름차순으로 정렬된 상태가 되며, 스택 내에서 특정 막대의 바로 이전 막대는 그 막대보다 왼쪽에 있으면서 높이가 작은 가장 오른쪽 막대가 된다. 즉, 직사각형의 넓이를 계산해야 될 때, 왼쪽 막대(스택에서 최상위 막대 바로 이전에 저장된 막대), 높이(스택의 최상위 막대), 오른쪽 막대(현재 보는 막대)를 모두 상수 시간에 알 수 있다는 뜻이다. 즉, 모든 막대를 한 번 씩 보면서 각 막대가 딱 한 번 씩 스택에 들어갔다 나오며, 중간 중간 직사각형의 넓이를 상수시간에 계산하기 때문에 전체 시간 복잡도는 $O(N)$ 이 된다.

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        heights.push_back(-1);
        stack<int> stk;
        stk.push(-1);
        int ans = 0;
        for(int i = 0; i < heights.size(); i++) {
            while(stk.size() > 1 && heights[i] < heights[stk.top()]) {
                int mid = stk.top();
                stk.pop();
                int left = left = stk.top();
                ans = max(ans, (i - left - 1) * heights[mid]);
            }
            stk.push(i);
        }
        return ans;
    }
};

사실 그림으로 설명하면 훨씬 이해가 쉬울텐데 그리기가 귀찮기 때문에 나중에 그림이 그리고 싶어졌을 때 첨부할 예정이다.

문제 링크

리트코드(LeetCode) - https://leetcode.com/problems/largest-rectangle-in-histogram/
백준 온라인저지(BOJ) - https://www.acmicpc.net/problem/6549

#

Comments

×